Sommario
La diffusione degli strumenti informatici e la parallela crescita della comunicazione attraverso le reti di calcolatori hanno posto con pressante urgenza il problema della sostituzione del tradizionale documento cartaceo con un equivalente strumento informatico. Il meccanismo universalmente adottato per costruire tale strumento è la firma digitale basata sulla crittografia a chiavi pubbliche. Vengono qui discussi a livello elementare i concetti fondamentali e le tecnologie su cui la firma digitale si basa.
La firma digitale
La firma digitale è una informazione che viene aggiunta ad un documento informatico al fine di garantirne integrità e provenienza. Sebbene l’uso per la sottoscrizione dei documenti formati su supporti informatici sia quello più naturale, essa può essere utilizzata per autenticare una qualunque sequenza di simboli binari, indipendentemente dal loro significato. Un esempio sempre più comune di questo uso generalizzato è l’aggiunta di firme digitali ai file contenuti nella memoria di massa di un sistema di elaborazione onde contrastare gli attacchi dei virus e degli hacker.
La principale differenza tra firma autografa e firma digitale sta nel fatto che la prima è direttamente riconducibile all’identità di colui che la appone, poiché la calligrafia è un elemento identificativo della persona, mentre la seconda non possiede questa proprietà. Per coprire questa deficienza si ricorre all’autorità di certificazione, il cui compito è quello stabilire, garantire e pubblicare l’associazione tra firma digitale e soggetto sottoscrittore.
Per contro, mentre l’associazione tra testo di un documento e la firma autografa è ottenuta esclusivamente attraverso il supporto cartaceo, la firma digitale è intrinsecamente legata ad testo a cui è apposta, tanto che i due oggetti possono essere fisicamente separati senza che per questo venga meno il legame esistente tra loro. Conseguenza di ciò è l’unicità della firma digitale, nel senso che a testi diversi corrispondono firme diverse e quindi, non ostante la sua perfetta replicabilità, è impossibile trasferirla da un documento ad un altro.
La base della firma digitale: la crittografia a chiavi pubbliche
I meccanismi di firma digitale poggiano essenzialmente sopra gli algoritmi crittografici a chiavi pubbliche, che sono detti anche a chiavi asimmetriche poiché utilizzano chiavi diverse per le operazioni di codifica e decodifica. La chiave di codifica Kc e quella di decodifica Kd vengono utilizzate all’interno delle rispettive funzioni C e D per trasformare la sequenza binaria che costituisce un messaggio M nel corrispondente messaggio cifrato X, risultando:
X=C(Kc,M) ; M=D(Kd,X)
La condizione più importante che deve essere soddisfatta affinché il sistema costituito dalla coppia di funzioni C e D e dalla coppia di chiavi Kc e Kd sia utilizzabile come sistema di cifratura a chiavi pubbliche è che la conoscenza della chiave pubblica Kp non consenta di determinare la chiave segreta Ks.
Algoritmo di Diffie-Hellman
Nel 1976 Diffie ed Hellman [DIHE76] hanno descritto un protocollo per lo scambio di una chiave segreta sopra un canale insicuro; tale meccanismo era stato inteso essenzialmente per risolvere il problema dell’avvio di un normale sistema di cifratura a chiavi simmetriche, quale il DES [FIPS46, FIPS81], ma in realtà ha posto le basi della crittografia a chiavi pubbliche.
Il protocollo, utilizzato da due interlocutori A e B, può essere descritto come segue:
In questo modo entrambi gli interlocutori possiedono la chiave K ma sopra il canale insicuro sono stati trasferiti solo N, s, samod N ed sbmod N che non consentono di ricostruire K. In realtà la determinazione di a noti s ed sa richiede la soluzione del problema del logaritmo discreto che consiste nella determinazione dell’intero che corrisponde al logaritmo in una base intera di un intero di cui è noto solo resto della divisione rispetto al modulo N. Tale problema è computazionalmente difficile.
Lo RSA
Proposto nel 1978 da Rivest, Shamir e Adleman [RSA78], da cui il nome, è il primo sistema di crittografia a chiavi pubbliche basato sui concetti proposti da Diffie ed Hellman ed è anche quello attualmente più diffuso ed utilizzato.
Il metodo si basa sulla fattorizzazione di interi di grandi dimensioni e per utilizzarlo ciascun interlocutore deve compiere le seguenti azioni:
Il messaggio cifrato X corrispondente ad un messaggio M si ottiene dalla relazione:
X=Mc mod N
mentre la decodifica avviene secondo la relazione:
Xd mod N = (Mc mod N)d mod N = Mcd mod N = M.
La sicurezza dello RSA è affidata alla difficoltà di determinare i fattori primi di un intero quando questo è molto grande, difficoltà che aumenta in modo esponenziale al crescere del numero di bit usati per la chiave.
Algoritmo di ElGamal
Più vicino dello stesso RSA all’impostazione di Diffie ed Hellman, di cui è di fatto un’estensione, è l’approccio proposto da ElGamal nel 1985 [ELGA85], nel quale ciascun interlocutore opera nel seguente modo:
La cifratura di un messaggio è un’operazione un po’ più complessa che nel caso dello RSA. Indicate con
a e b le chiavi segrete scelte da A e B, cosicché Kpa = sa mod N e Kpb = sb mod N risultano essere le rispettive chiavi pubbliche, se A vuole inviare un messaggio a B deve effettuare le seguenti operazioni:Il destinatario B, che riceve x1 = sh mod N e possiede
b , calcola a sua volta K = (sh)b e recupera M dividendo x2 per il valore di K appena ricavato.In pratica il sistema di ElGamal può essere riguardato come un cifrario simmetrico nel quale però la chiave di codifica, da utilizzare anche per la decodifica, viene generata dinamicamente e comunicata, sfruttando il protocollo di scambio di Diffie-Hellman, insieme con il messaggio.
Il meccanismo di cifrare i messaggi con un sistema simmetrico, generando in modo casuale per ciascuno di essi una nuova chiave che viene allegata, cifrata mediante un sistema a chiavi pubbliche, al messaggio stesso, viene largamente utilizzato per sopperire alla intrinseca inefficienza dei cifrari asimmetrici e consentire la cifratura in linea dei messaggi scambiati in un sistema di comunicazione.
La sicurezza del sistema di ElGamal è ovviamente uguale a quella del protocollo di Diffie-Hellman e si basa sulla complessità di soluzione del problema del logaritmo discreto.
Le curve ellittiche
Sono stati proposti sistemi crittografici a chiavi asimmetriche che possono essere riguardati come una generalizzazione di quelli sopra descritti. Infatti, dal punto di vista matematico un tale sistema può essere considerato come una trasformazione sopra gli elementi di un insieme che possiede la struttura di gruppo algebrico, è quindi possibile ottenere sistemi diversi e con differenti caratteristiche di sicurezza sostituendo l’insieme di base.
In particolare è possibile utilizzare come gruppo di base l’insieme dei punti di una curva ellittica definita su di un campo finito, che costituisce un gruppo abeliano [MENE93]. Il vantaggio principale che si ottiene con tale approccio è che una scelta opportuna della curva utilizzata dal sistema di cifratura consente di ottenere una complessità matematica del problema della rottura del codice nettamente superiore a quella dei problemi della fattorizzazione di un intero di grandi dimensioni o del calcolo del logaritmo discreto.
Uso degli algoritmi crittografici asimmetrici per la firma digitale
I metodi crittografici a chiavi pubbliche possono essere utilizzati per costruire strumenti per la firma digitale, la differenza principale tra le due applicazioni risiede nel ruolo delle chiavi. Nella crittografia la chiave pubblica viene utilizzata per la cifratura mentre il destinatario usa quella privata per recuperare il messaggio. Nella firma il messaggio M non è in genere cifrato ed è direttamente disponibile per il destinatario, viceversa l’autore utilizza la funzione di cifratura C e la chiave privata Ks per generare il valore di X che, aggiunto ad M, ne certifica la provenienza grazie alla segretezza della chiave privata. X costituisce la firma digitale di M. Chiunque può accertare la provenienza del messaggio utilizzando la chiave pubblica Kp per verificare che il valore della firma corrisponda al messaggio grazie alla relazione:
D(Kp,X) = M
In realtà la verifica della corrispondenza tra firma e messaggio garantisce solo che questa è stata generata mediante la chiave privata corrispondente a Kp, occorre perciò assicurare per altra via la corrispondenza tra chiavi e soggetto autore del messaggio. A tale scopo viene utilizzata la "Autorità di Certificazione" (AC), la quale, dopo aver accertato dell’identità del possessore della chiave privata e della corrispondenza tra questa e quella pubblica, certifica l’identità del possessore della chiave privata (a meno della rottura della sua segretezza). L’uso dell’autorità di certificazione consente di raggiungere, oltre la certezza dell’identità dell’autore di un messaggio, anche l’impossibilità da parte di questi di ripudiare i messaggi da lui generati; infatti, essendo l’unico detentore della chiave privata è anche l’unico soggetto in grado di generare firme verificabili con la corrispondente chiave pubblica.
Sebbene qualunque sistema crittografico a chiavi pubbliche possa essere utilizzato per generare firme elettroniche, un aspetto di grande importanza pratica consiste nella disponibilità di algoritmi di codifica e decodifica specificamente adatti per la generazione e la verifica della firma. Infatti, dato che di norma il messaggio M è direttamente disponibile per il destinatario insieme con X, non si ha alcun interesse nella possibilità di ricostruire M da X. Ciò consente di ridurre molto la lunghezza di X a beneficio dell’efficienza delle operazioni naturalmente lente di codifica e decodifica.
C’è un altro aspetto di notevole interesse pratico legato alla disponibilità di algoritmi diversi per la cifratura e la firma. Il governo americano impedisce l’esportazione di software di cifratura che utilizzi chiavi di lunghezza tale da garantire la resistenza del cifrario per un periodo relativamente lungo. Un’analoga limitazione non si applica agli algoritmi di generazione e verifica di firme elettroniche a patto che questi non siano modificabili in modo da renderli utilizzabili per la cifratura.
Lo RSA
L’uso dello RSA per generare firme elettroniche [RSA78] si basa semplicemente sull’inversione del ruolo delle chiavi rispetto a quello per assicurare la riservatezza, la principale differenza tra le due applicazioni sta nel fatto che per la firma si evita di applicare l’operazione di codifica all’intero testo. Ciò è particolarmente conveniente vista la complessità, e quindi la lentezza, delle operazioni coinvolte.
In pratica il testo da firmare viene "compresso" in una sorta di "riassunto", che viene spesso riferito come "impronta", mediante una opportuna funzione di hash progettata in modo da rendere trascurabile la probabilità che da testi diversi si possa ottenere il medesimo valore. La dimensione del riassunto è fissa ed è molto più piccola di quella del messaggio originale; infatti è dell’ordine del centinaio di bit, ciò rende la generazione della firma, effettuata a partire dall’impronta anziché dal testo, estremamente più rapida. Qualche dettaglio su come venga realizzata questa operazione verrà fornito nella sezione successiva.
ElGamal
L’algoritmo proposto da ElGamal per la firma digitale [ELGA85] è alquanto diverso da quello già citato destinato alla cifratura. Per generare la firma di un testo M occorre effettuare le seguenti operazioni:
La verifica della firma viene effettuata in base alla relazione:
sM = Kpu uv mod N
La sicurezza del sistema è basata sul fatto che la determinazione di una coppia di valori (u,v) che soddisfi la precedente equazione richiede la soluzione del problema del logaritmo discreto nel caso in cui si fissi u e si cerchi di determinare v di conseguenza; nel caso opposto, ossia fissando v e cercando di calcolare u, si incappa in una congruenza esponenziale mista per la quale non sono noti algoritmi efficienti di soluzione.
Schnorr
Il metodo di generazione della firma dovuto a Schnorr [SCHN91] è analogo a quello di ElGamal, dal quale differisce essenzialmente per l’introduzione di una funzione di hash H che associa a ciascun messaggio ed a ciascuna chiave un intero in un intervallo di ampiezza predefinita T.
La procedura di generazione della firma è la seguente:
La verifica si effettua nel modo seguente:
Anche la sicurezza del sistema di firma di Schnorr, come quello di ElGamal, è legata alla complessità di soluzione del problema del calcolo del logaritmo discreto. Il vantaggio principale che questo algoritmo presenta rispetto al precedente è la possibilità di scegliere la dimensione della firma selezionando opportunamente l’ampiezza T del codominio della funzione di hash.
DSS
Il Digital Signature Standard [FIPS186], proposto dal NIST (National Institute of Standard and Technology) nel 1991, è sostanzialmente una variante del metodo di Schnorr in cui la funzione di hash H ha come unico argomento il messaggio e quindi il suo valore non dipende dalla chiave di cifratura. L’utilizzazione del sistema richiede preliminarmente la generazione delle chiavi secondo la seguente procedura:
Ottenute le chiavi, la generazione della firma per un messaggio M si ottiene nel modo seguente:
La verifica viene condotta mediante la seguente procedura:
Il DSS è di fatto una variante dell’algoritmo di Schnorr e quindi deve la sua robustezza alla complessità del problema del logaritmo discreto, tuttavia la predefinizione dei limiti di variabilità dei parametri di base ha attirato numerose critiche riguardo l’effettiva sicurezza raggiungibile.
Il processo di firma digitale
Il processo di firma digitale richiede che l’utente effettui una serie di azioni preliminari necessarie alla predisposizione delle chiavi utilizzate dal sistema di crittografia su cui il meccanismo di firma si basa; in particolare occorre:
Una volta espletate tali operazioni, per tutta la durata del periodo di validità della certificazione della chiave pubblica, l’utente è in grado di firmare elettronicamente un numero qualunque di documenti sfruttando la sua chiave segreta Ks,. Tale periodo può essere interrotto prima del suo termine naturale dalla revoca della certificazione, che di norma viene effettuata su richiesta del proprietario qualora egli ritenga che la segretezza della sua chiave privata sia stata compromessa, ma che potrebbe avvenire anche per iniziativa dell’AC, ad esempio perché l’utente non ha più titolo per l’uso della chiave.
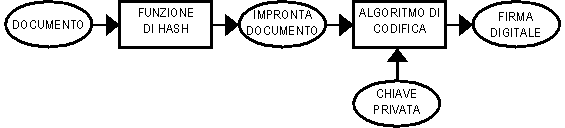
Il processo di sottoscrizione, schematicamente mostrato nella Figura 1, consta di una sequenza di tre operazioni:

Figura 1 - Generazione della firma digitale
Le fasi di tale processo e quelle preliminari di registrazione dell’utente e certificazione delle chiavi verranno ora ordinatamente analizzate con qualche dettaglio.
Registrazione dell’utente
La registrazione dell’utente presso una autorità di certificazione ha il duplice scopo di rendere questa certa della sua identità ed instaurare con esso un canale di comunicazione sicuro attraverso il quale verranno fatte viaggiare le chiavi pubbliche di cui viene richiesta la certificazione. All’atto della registrazione l’autorità di certificazione attribuisce all’utente un identificatore, di cui viene garantita l’univocità, attraverso il quale sarà possibile a chiunque reperire in modo diretto e sicuro i certificati rilasciati al soggetto all’interno dei cataloghi pubblici in cui questi sono registrati.
La registrazione avviene attraverso la seguente procedura:
La necessità di utilizzare un canale sicuro di comunicazione tra utente ed autorità di certificazione, asserita al precedente punto 4, non è motivata da esigenze di riservatezza, infatti su tale canale viaggiano essenzialmente chiavi pubbliche, ma di autenticità. Infatti l’autorità di certificazione, quando riceve una richiesta da un utente, deve avere la certezza che questa provenga effettivamente da lui e non da qualcuno che lo sta impersonando. Ciò non può essere sempre ottenuto con la normale firma digitale, basti pensare al caso della richiesta di certificazione della prima chiave oppure a quella di revoca di una chiave. Analoghi problemi sorgono per l’utente nei confronti dell’AC quando, ad esempio, questi abbia necessità di verificare la validità della chiave di certificazione che potrebbe, in un caso estremo, essere stata revocata.
In realtà la possibilità di verificare con certezza la validità della chiave pubblica di certificazione, e quindi la disponibilità di un canale sicuro attraverso cui effettuare tale operazione, è l’elemento base per garantire l’affidabilità dell’intero sistema di firma digitale, infatti dalla validità di questa può essere fatta scaturire la garanzia di validità di tutte le altre.
Generazione della coppia di chiavi
L’utente, mediante un programma adatto al sistema crittografico adottato, genera una coppia di chiavi. Una di esse, quella da utilizzare per le operazioni di cifratura e quindi per la generazione della firma, sarà mantenuta segreta ed assumerà il ruolo di Ks. L’altra, destinata alla verifica, verrà resa pubblica attraverso la certificazione e corrisponderà perciò a Kp.
Certificazione della chiave pubblica
La certificazione della chiave pubblica ha lo scopo di rassicurare chiunque riceva un documento correttamente firmato, circa l’identità del soggetto che ha apposto la firma. L’operazione avviene attraverso tre passi:
Registrazione della chiave pubblica
Una volta emesso, il certificato può essere reso disponibile in uno o più cataloghi ai quali può accedere chiunque abbia bisogno di accertare la validità di una sottoscrizione digitale. Questa operazione viene di norma effettuata, almeno per i cataloghi di sua competenza, dalla AC, contestualmente all’emissione.
Generazione dell’impronta
Al testo da firmare viene applicata una funzione di hash appositamente studiata che produce, secondo il meccanismo sinteticamente mostrato nella Figura 2, una stringa binaria di lunghezza costante e piccola, normalmente 128 o 160 bit. La funzione di hash assicura l’unicità di tale stringa, nel senso che a due testi diversi non corrisponde la medesima impronta. Sono disponibili diversi algoritmi di generazione, quali, ad esempio, MD2 [KALI92], MD4 [RIVE90] e MD5 [RIVE92], originariamente progettati per operare in combinazione con lo RSA ma utilizzabili con qualsiasi cifrario. Sono disponibili anche algoritmi di hash per i quali è in corso la standardizzazione ufficiale da parte organismi internazionali, ne sono un esempio il RIPEMD a 128 e 160 bit ed il Secure Hash Algorithm (SHA-1) [JTC196].
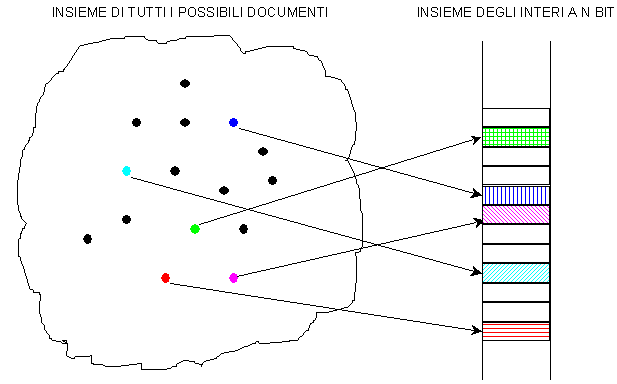
Figura 2 - Generazione del'impronta
L’utilità dell’uso dell’impronta è duplice, in primo luogo consente di evitare che per la generazione della firma sia necessario applicare l’algoritmo di cifratura, che è intrinsecamente inefficiente, all’intero testo che può essere molto lungo. Inoltre consente l’autenticazione, da parte di una terza parte fidata, della sottoscrizione di un documento senza che questa venga a conoscenza del suo contenuto. Una tipica situazione in cui si sfruttano tali caratteristiche dell’impronta è la marcatura temporale che verrà discussa più avanti.
Generazione della firma
La generazione della firma consiste semplicemente nella cifratura, con la chiave segreta Ks, dell’impronta digitale generata il precedenza. In questo modo la firma risulta legata da un lato, attraverso la chiave segreta usata per la generazione, al soggetto sottoscrittore, e dall’altro, per il tramite dell’impronta, al testo sottoscritto.
In realtà l’operazione di cifratura viene effettuata, anziché sulla sola impronta, su una struttura di dati che la contiene insieme con altre informazioni utili, quali ad esempio l’indicazione della funzione hash usata per la sua generazione. Sebbene tali informazioni possano essere fornite separatamente rispetto alla firma, la loro inclusione nell’operazione di codifica ne garantisce l’autenticità.
Apposizione della firma
La firma digitale generata al passo precedente viene aggiunta in una posizione predefinita, normalmente alla fine, al testo del documento. Normalmente, insieme con la firma vera e propria, viene allegato al documento anche il valore dell’impronta digitale ed eventualmente il certificato da cui è possibile recuperare il valore della chiave pubblica.
È evidente che essendo il legame tra firma e documento, stabilito attraverso l’impronta, di natura puramente logica, la firma stessa e le informazioni aggiuntive eventualmente ad essa associate possono essere registrate e gestite in modo del tutto separato rispetto al testo sottoscritto; in particolare possono trovarsi su supporti e sistemi di elaborazione del tutto indipendenti tra loro.
Verifica della firma digitale
L’operazione di verifica della firma digitale, mostrata schematicamente in Figura 3, viene effettuata ricalcolando, con la medesima funzione di hash usata nella fase di sottoscrizione, il valore dell’impronta e controllando che il valore così ottenuto coincida con quello generato per decodifica della firma digitale stessa.

Figura 3 - Verifica della firma digitale
Per facilitare l’operazione di verifica viene di solito allegato al documento firmato anche il certificato relativo alla chiave pubblica. Ciò non sarebbe strettamente necessario, dato che questo dovrebbe essere sempre recuperabile dal registro pubblico del certificatore, tuttavia, specie nel caso in cui la struttura di dati che costituisce la firma è povera di informazioni, tale ricerca potrebbe essere notevolmente onerosa, soprattutto se il registro in cui cercare non è univocamente determinato.
Al contrario, la disponibilità del certificato consente di disporre immediatamente delle seguenti informazioni, difficilmente contenute nella firma:
La presenza di un certificato formalmente valido non può però esimere dalla verifica presso il certificatore, è infatti possibile che sia sopraggiunta una revoca della chiave di sottoscrizione, o, all’estremo, di quella di certificazione.
Marcatura temporale
Qualora sia necessario attribuire ad un documento certezza circa il momento in cui questo è stato redatto ed è divenuto valido, si ricorre alla sua marcatura temporale. Questa consiste nella generazione da parte di una terza parte fidata, normalmente una AC, di una ulteriore firma digitale aggiuntiva rispetto a quella del sottoscrittore.
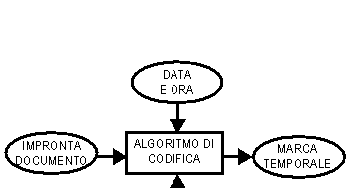
Figura 4 - Generazione della marca temporale
L’operazione, rappresentata schematicamente nella Figura 4, avviene secondo la seguente procedura:
La marcatura temporale presenta interessanti analogie con l'autenticazione e può essere usata per garantire che un documento non venga in secondo tempo sostituito con uno diverso da parte dell’autore stesso.
La standardizzazione
Sotto la spinta delle applicazioni commerciali, ed in particolare di quelle bancarie, sono stati sviluppati numerosi standard, tanto de iure che de facto, relativi all’uso delle tecniche crittografiche, che possono trovare applicazione per la sottoscrizione digitale.
Nell’ambito della standardizzazione ufficiale, un ruolo determinante é ovviamente giocato dall’International Standard Organization, che costituisce l’ente normatore primario a livello internazionale. Tale organismo ha emanato numerose norme in campo crittografico, destinate principalmente al settore bancario ed a quello della tecnologia dell’informazione, le più significative sono elencate nell’Appendice. Si tenga presente che, per la normazione in campo informatico, l’ISO opera in congiunzione con l’International Electrical Commission (IEC), con la quale ha costituito un apposito comitato tecnico congiunto, la Joint Technical Comittee n° 1 (JTC1).
Accanto all’ISO, ed in modo coordinato con esso, opera l’International Telecommunication Union (ITU), che ha sostituito lo storico CCITT ed emette "raccomandazioni" che hanno valore di norme primarie nei settori delle telecomunicazioni (ITU-T) e della radiodiffusione (ITU-R). Da esso i provengono le raccomandazioni X.400 ed X.500 che hanno una importanza fondamentale per i sistemi di messaggistica elettronica. In particolare alla famiglia X.500 appartiene la raccomandazione X.509 verso cui stanno convergendo tutti i sistemi di autenticazione e firma digitale quale standard per i certificati. Il coordinamento tra ITU ed ISO è, almeno per le questioni che hanno riflessi sulla firma digitale, molto stretto. Infatti l’intera famiglia X.500 è emanata in modo congiunto, ossia a ciascuna "raccomandazione" ITU-T corrisponde uno "standard internazionale" ISO tali che il testo di entrambi è esattamente lo stesso. Nell’Appendice é riportata la tabella di corrispondenza tra i due tipi di norme, si noti la diversa tecnica di numerazione usata dai due enti: l’intera famiglia ITU-T è associata ad un’unica norma ISO/IEC, la 9594, con ciascuna raccomandazione in corrispondenza di una parte di questo standard.
Accanto agli enti normatori internazionali non può essere ignorato il ruolo delle maggiori organizzazioni di standardizzazione americane. Il National Institute of Standards and Technology (NIST) è già stato ricordato per la definizione del Digital Signature Standard (DSS). Ad esso si affianca lo American National Standards Institute (ANSI), ben noto per i suoi standard largamente diffusi nel mondo dell’informatica, che ha emesso numerose norme per il settore finanziario tra cui vale la pena ricordare la X9.30.1, che definisce il Digital Signature Algorithm (DSA), e la X9.30.2, che specifica il Secure Hash Algorithm (SHA-1) recepito anche dall’ISO nella norma ISO/IEC CD 10118-3 [JTC196].
Deve essere infine menzionato lo Institute of Electrical and Electronics Engineers (IEEE), al quale si deve tra l’altro la standardizzazione di Ethernet, che sta compiendo un notevole sforzo per sviluppare uno standard unico ed integrato comprendente tutti gli algoritmi asimmetrici attualmente disponibili, da quelli basati sulla fattorizzazione degli interi, a quelli che sfruttano il problema del logaritmo discreto, a quelli che usano le proprietà delle curve ellittiche. Tale progetto di standard viene indicato con la sigla P1363.
Parallelamente agli standard ufficiali, e per alcuni versi in anticipo rispetto a questi, sono stati sviluppati e si sono affermati alcuni standard di fatto che non possono essere trascurati, soprattutto perché possono vantare un numero di implementazioni ed una quantità di utenti superiore a quella degli standard de iure. In tale ambito deve essere ricordato in primo luogo Pretty Good Privacy (PGP), cui deve essere riconosciuto il merito di aver diffuso la crittografia a chiavi pubbliche, sia pure più con lo scopo di proteggere la riservatezza della comunicazione che per l’autenticazione dei documenti. Il pacchetto, originariamente sviluppato al Massachussets Institute of Technology (MIT) e finora di libero utilizzo per scopi non commerciali, è attualmente lo strumento maggiormente usato in ambito privato ed anche il primo a consentire l’uso, accanto al tradizionale RSA, del DSS.
Per la diffusione nei prodotti commerciali deve essere infine considerato il Public Key Crypto System (PKCS), un insieme di specifiche tecniche pubblicate dalla RSA Inc. con lo scopo di fornire uno strumento atto a garantire l’interoperabilità dei prodotti utilizzanti il cifrario di Rivest Shamir e Adleman.
In definitiva gli standard attinenti la firma digitale maggiormente rilevanti a livello europeo possono essere inquadrati in quattro filoni principali:
Gli standard utilizzati nel settore bancario rivestono particolare importanza poiché sono quelli maggiormente consolidati e collaudati; d’altra parte essi si presentano in realtà come una molteplicità di norme eterogenee e sostanzialmente incompatibili tra loro, sviluppate sotto la spinta di specifiche applicazioni, quali il trasferimento di ordinativi, l’effettuazione di transazioni con carta di credito e così via. L’integrazione dei servizi e dei vari circuiti bancari ha comunque portato allo sviluppo di strumenti di interoperabilità e alla progressiva convergenza verso le norme di maggiore generalità.
L’eterogeneità presente nel settore si manifesta in modo eclatante nella sostanziale incompatibilità tra norme emanate dalla stessa organizzazione, come accade nel caso degli standard internazionali emanati dall’ISO per il settore bancario da un lato e per quello della tecnologia dell’informazione dall’altro. Questi ultimi, più recenti, costituiscono la base su cui costruire sistemi interoperabili e durevoli nel tempo. Un fatto che conforta questa prospettiva é la progressiva convergenza, nel settore più maturo della tecnologia, quello dei certificati, verso lo X.509 come standard di base unico, eventualmente esteso in modo diverso secondo le particolari necessità, ma comunque universalmente supportato nelle caratteristiche essenziali.
In effetti fino ad oggi le tecniche crittografiche, anche a chiavi pubbliche, sono state utilizzate essenzialmente per assicurare la riservatezza della comunicazione e quindi la compatibilità e l’interoperabilità erano considerate caratteristiche di secondaria importanza, se non addirittura potenzialmente pericolose. Il ribaltamento della prospettiva introdotto dalla firma digitale, che deve garantire l’autenticità di un documento di fronte a chiunque e non solo per il diretto destinatario, porterà, come è successo nei protocolli di comunicazione, ad una rapida convergenza verso gli standard maggiormente efficaci.
Appendice
Principali norme ISO
L’elenco che segue riporta quelli più direttamente correlati con le problematiche connesse alla firma digitale.
ISO/IEC 8372:1987 Modes of operation for a 64-bit block cipher algorithm.
ISO/IEC 8731-1:1988 Banking - Approved Algorithms for Message Authentication - Part 1: DEA
ISO/IEC 8731-2:1992 Banking - Approved Algorithms for Message Authentication - Part 2: Message Authentication Algorithm
ISO/IEC 8732:1988 Banking - Key management (wholesale)
ISO/IEC 9796:1991 Information technology - Security techniques - Digital signature scheme giving message recovery.
ISO/IEC 9796-2:1997 Information technology - Security techniques - Digital signature scheme giving message recovery – Part 2: Mechanisms Using a Hash-Function
ISO/IEC 9797:1994 Information technology - Security techniques - Data integrity mechanism using a cryptographic check function employing a block cipher algorithm.
ISO/IEC 9798-1:1991 Information technology - Security techniques - Entity authentication mechanism - Part 1: General model (in revisione come DIS).
ISO/IEC 9798-2:1994 Information technology - Security techniques - Entity authentication mechanism - Part 2: Mechanisms using symmetric encipherment algorithms.
ISO/IEC 9798-3:1993 Information technology - Security techniques - Entity authentication mechanism - Part 3: Mechanisms using a public key algorithm.
ISO/IEC 9798-4:1995 Information technology - Security techniques - Entity authentication mechanism - Part 4: Mechanisms using a cryptographic check function.
ISO/IEC WD 9798-5:1995 Information technology - Security techniques - Entity authentication mechanism - Part 5: Mechanisms using zero knowledge techniques.
ISO/IEC 9979:1991 Data cryptografic techniques - Procedures for the registration of cryptographic algorithms.
ISO/IEC 10116:1991 Information technology - Security techniques - Modes of operation for an n-bit block cipher algorithm (in revisione come DIS).
ISO/IEC 10118-1:1994 Information technology - Security techniques - Hash-functions - Part 1: General.
ISO/IEC 10118-2:1994 Information technology - Security techniques - Hash-functions - Part 2: Hash-functions using an n-bit block cipher algorithm.
ISO/IEC CD 10118-3 Information technology - Security techniques - Hash-functions - Part 3: Dedicated hash-functions.
ISO/IEC CD 10118-4 Information technology - Security techniques - Hash-functions - Part 4: Hash-functions using modular arithmetic.
ISO/IEC 10126-1:1991 Banking - Procedures for message encipherment (wholesale) - Part 1: General principles.
ISO/IEC 10126-2:1991 Banking - Procedures for message encipherment (wholesale) - Part 2: DEA algorithm.
ISO/IEC 11166-1:1994 Banking - Key management by means of asymmetric algorithms - Part 1: Principles, procedures and formats.
ISO/IEC 11166-2:1994 Banking - Key management by means of asymmetric algorithms - Part 2: Approved algorithms using the RSA cryptosystem.
ISO 11568-1:1994 Banking - Key management (retail) - Part 1: Introduction to key management.
ISO 11568-2:1994 Banking - Key management (retail) - Part 2: Key management techniques for symmetric ciphers.
ISO 11568-3:1994 Banking - Key management (retail) - Part 3: Key life cycle for symmetric ciphers.
ISO DIS 11568-4 Banking - Key management (retail) - Part 4: Key management techniques for public key cryptosystems.
ISO DIS 11568-5 Banking - Key management (retail) - Part 5: Key life cycle for public key cryptosystems.
ISO DIS 11568-6 Banking - Key management (retail) - Part 6: Key management schemes.
ISO/IEC DIS 11770-1 Information technology - Security techniques - Key management - Part 1: Framework.
ISO/IEC 11770-2:1996 Information technology - Security techniques - Key management - Part 2: Mechanism using symmetric techniques.
ISO/IEC DIS 11770-3 Information technology - Security techniques - Key management - Part 3: Mechanism using asymmetric techniques.
Corrispondenza ITU-T X.5xx e ISO/IEC 9594
|
ITU-T |
ISO/IEC |
Titolo |
|
X.500 |
9594-1 |
Information technology - Open Systems Interconnection - The Directory: Overview of concepts, models and services |
|
X.501 |
9594-2
|
Information technology - Open Systems Interconnection - The Directory: Models |
|
X.509 |
9594-8
|
Information technology - Open Systems Interconnection - The Directory: Authentication framework |
|
X.511 |
9594-3
|
Information technology - Open Systems Interconnection - The Directory: Abstract service definition |
|
X.518 |
9594-4 |
Information technology - Open Systems Interconnection - The Directory: Procedures for distributed operation |
|
X.519 |
9594-5
|
Information technology - Open Systems Interconnection - The Directory: Protocol specifications |
|
X.520
|
9594-6
|
Information technology - Open Systems Interconnection - The Directory: Selected attribute types |
|
X.521
|
9594-7
|
Information technology - Open Systems Interconnection - The Directory: Selected object classes |
|
X.525
|
9594-9
|
Information technology - Open Systems Interconnection - The Directory: Replications |
|
X.530
|
9594-10
|
Information technology - Open Systems Interconnection - The Directory: Use of systems management for administration of the Directory |
Riferimenti